jupyter notebookで野球データをビジュアライズ part 2

MAGAZINE

ルーターマガジン

データ/フォーマット

jupyter notebookで野球データをビジュアライズ part 2

2018.11.01

Pocket

日本シリーズ開幕！！

こんにちは！
ルーターエンジニアのohkabeです。日本シリーズが開幕しました。
前回に引き続き野球のデータをjupyter notebookでビジュアライズします。

下準備

以下のモジュールを使用しますのでインポートしておきましょう。

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

今回のデータは以下のリンクからお借りしました。
コードの書き方も参考にしています。

https://github.com/Shinichi-Nakagawa/pitchpx-example-pitchfx
MIT License

Copyright (c) 2016 Shinichi nakagawa
https://github.com/Shinichi-Nakagawa/pitchpx-example-pitchfx/blob/master/LICENSE

ダルビッシュ投手の配球をmatplotlibで可視化

今回はダルビッシュ選手の実際の投球データを使用し、matplotlibで散布図にします。
まずはデータフレームを読み込み、概要を見てみましょう。

df_src = pd.read_csv("https://raw.githubusercontent.com/Shinichi-Nakagawa/pitchpx-example-pitchfx/master/datasets/yu_darvish_201608170_pitch.csv")
df = df_src[['px', 'pz', 'pitch_type', 'start_speed', 'pa_ball_ct','pa_strike_ct']]

# 球速をマイルからキロに直す  
df["start_speed"] = df["start_speed"] * 1.61
df.head()

	px	pz	pitch_type	start_speed	pa_ball_ct	pa_strike_ct
0	0.764	0.693	FF	146.188	0	0
1	-0.111	3.403	FF	144.739	1	0
2	0.547	2.286	FF	146.993	0	0
3	-2.332	3.216	FT	145.222	0	1
4	0.252	3.430	SL	126.224	1	1

カラムは左から順に、

投球の水平位置
投球の垂直位置
球種
球速
ボールカウント
ストライクカウント

です。
球種の略記は以下のように対応しています。

PITCH_TYPES = {
    'CU': 'Curveball',
    'FC': 'Cut Fastball',
    'FF': 'four-seam Fastball',
    'FS': 'Split-finger Fastball',
    'FT': 'two-seam Fastball',
    'SL': 'Slider',
}

ではここで、どの球種をよく投げるのか見てみましょう。
pandasのvalue_counts()関数を使うと、値ごとに回数を数えてくれます。

df["pitch_type"].value_counts()

/* FF    39
/* FT    21
/* SL    14
/* FC    13
/* CU     9
/* FS     3
/* Name: pitch_type, dtype: int64

もっとも多いのがFF(フォーシーム)で、39回投げています。
value_counts(normalize=True)とすると割合で出力してくれます。

df["pitch_type"].value_counts(normalize=True)

/* FF    0.393939
/* FT    0.212121
/* SL    0.141414
/* FC    0.131313
/* CU    0.090909
/* FS    0.030303
/* Name: pitch_type, dtype: float64

次に球速の密度分布を見てみましょう。

ax = sns.distplot(df["start_speed"])

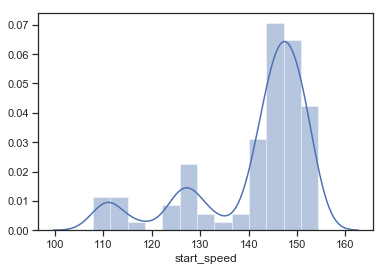
155キロから110キロの落差があるようです。

散布図の作成

def get_marker(pitch_type):
    if pitch_type == 'FF':
        return 'o'
    elif pitch_type == 'FT':
        return '3'
    elif pitch_type == 'FC':
        return '4'
    elif pitch_type == 'FS':
        return '1'
    elif pitch_type  == 'CU':
        return '$◢$'
    elif pitch_type == 'SL':
        return '>'
    return 'H'

fig = plt.figure(figsize=(13,9))

ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('px')
ax.set_xlim((-3.0, 3.0))
ax.set_ylabel('pz')
ax.set_ylim((0.0, 5.0))
ax.grid(True)

# ストライクゾーン
ax.vlines(-0.8, ymin=1.5, ymax=3.32)
ax.vlines(0.8, ymin=1.5, ymax=3.32)
ax.hlines(1.5, xmin=-0.8, xmax=0.8)
ax.hlines(3.32, xmin=-0.8, xmax=0.8)

for key, grp in df.groupby('pitch_type'):
    c = grp['start_speed']
    marker = get_marker(key)
    label = PITCH_TYPES[key]
    ax = plt.scatter(grp['px'],grp['pz'],c=c,cmap="jet",marker=marker,label=label, alpha=0.7)
    plt.clim(df['start_speed'].min(),df['start_speed'].max())


plt.colorbar()
plt.legend(bbox_to_anchor=(1, 1))
plt.show()

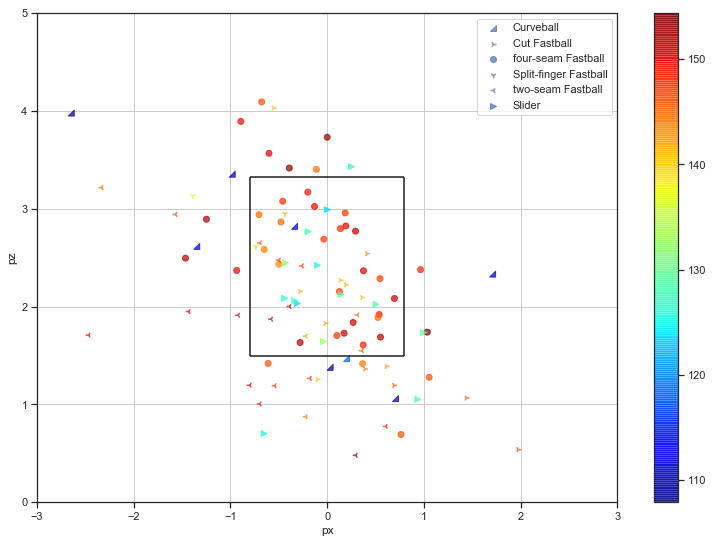
この図は球種、速度、コースをキャッチャー視点でグラフ化したものです。
色が球速、マーカーが球種を表しています。
真ん中の四角がストライクゾーンです。
ぱっと見、右上には投げないというのが見えますが、これは大きな特徴ではないでしょうか。
しかし、このままではあまりにも乱雑なプロットなので、よく分かりません。
次は球種別にデータを整理して、グラフを分解して見ます。

球種でグラフを分解

pandasのgroupbyメソッドで球種に対してグループ分けを行い、描画します。

fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(16, 8))

for (key, grp),ax in zip(df.groupby('pitch_type'),axes.flat):
    ax.title.set_text(PITCH_TYPES[key])
    ax.set_xlim((-3.0, 3.0))
    ax.set_ylim((0.0, 5.0))
    ax.grid(True)

    ax.vlines(-0.8, ymin=1.5, ymax=3.32)
    ax.vlines(0.8, ymin=1.5, ymax=3.32)
    ax.hlines(1.5, xmin=-0.8, xmax=0.8)
    ax.hlines(3.32, xmin=-0.8, xmax=0.8)

    c = grp['start_speed']
    marker = get_marker(key)
    im = ax.scatter(grp['px'],grp['pz'],c=c,cmap="jet",marker=marker, alpha=1,
                  vmin=df['start_speed'].min(), vmax=df['start_speed'].max())

fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.83, 0.15, 0.02, 0.7])
im.set_clim(vmin=df['start_speed'].min(), vmax=df['start_speed'].max())
cbar = fig.colorbar(im, cax=cbar_ax)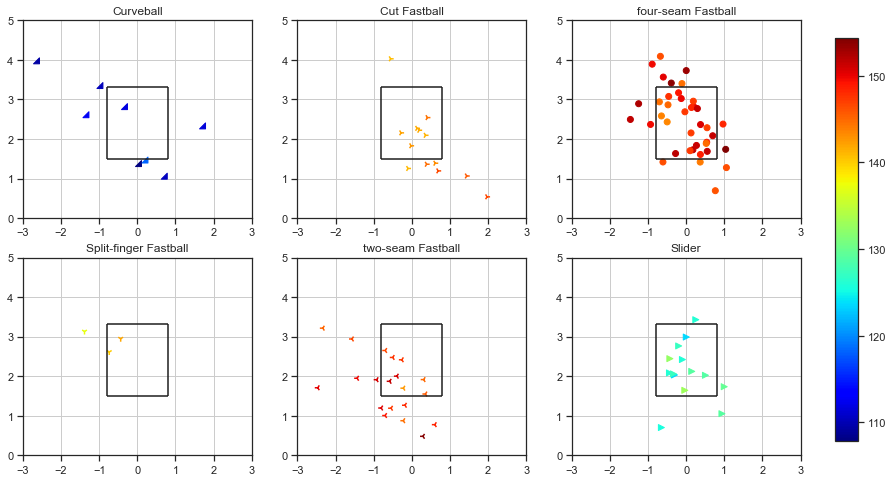

どうでしょうか。
だいぶスッキリして見えます。
こうして見ると、フォーシーム(直球)とツーシーム(左に曲がる)とカットボール(右に曲がる)がほぼ同じ速度です。
打者から見ると、直球と左右の変化球で、見分けがつかない三択になっているのでしょう。
カーブは遅いですね。

配給の特徴としては

フォーシームは左上から右下の対角線上
ツーシームは左下
スライダーは真ん中に寄る

という癖が有るように見えますね。

ボールカウントでグラフを分解

さらにボールカウントの情報を与えて配給を分解して見ましょう。

# ストライク * ボールの組み合わせで12個のグラフを作りたい  
fig, axes = plt.subplots(nrows=4, ncols=3, figsize=(32, 32))

count = 0

for ax in axes.flat:
    # 列がストライク、行がボールのカウントとなるように配置  

    strike = count % 3
    ball = count // 3
    tmp = df[(df['pa_ball_ct'] == ball) & (df['pa_strike_ct'] == strike)]
    count +=1

    ax.title.set_text("Strike{}-Ball{}".format(strike, ball))
    ax.set_xlim((-3.0, 3.0))
    ax.set_ylim((0.0, 5.0))
    ax.grid(True) 

    ax.vlines(-0.8, ymin=1.5, ymax=3.32)
    ax.vlines(0.8, ymin=1.5, ymax=3.32)
    ax.hlines(1.5, xmin=-0.8, xmax=0.8)
    ax.hlines(3.32, xmin=-0.8, xmax=0.8)

    for key, grp in tmp.groupby('pitch_type'):
          marker = get_marker(key)
          c = grp['start_speed']
          label = PITCH_TYPES[key]
          im = ax.scatter(grp['px'],grp['pz'],c=c,cmap="jet",marker=marker,label=label,
                          alpha=1, vmin=df['start_speed'].min(), vmax=df['start_speed'].max())

    ax.legend(bbox_to_anchor=(1, 1))

fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.83, 0.15, 0.02, 0.7])
im.set_clim(vmin=df['start_speed'].min(), vmax=df['start_speed'].max())
cbar = fig.colorbar(im, cax=cbar_ax)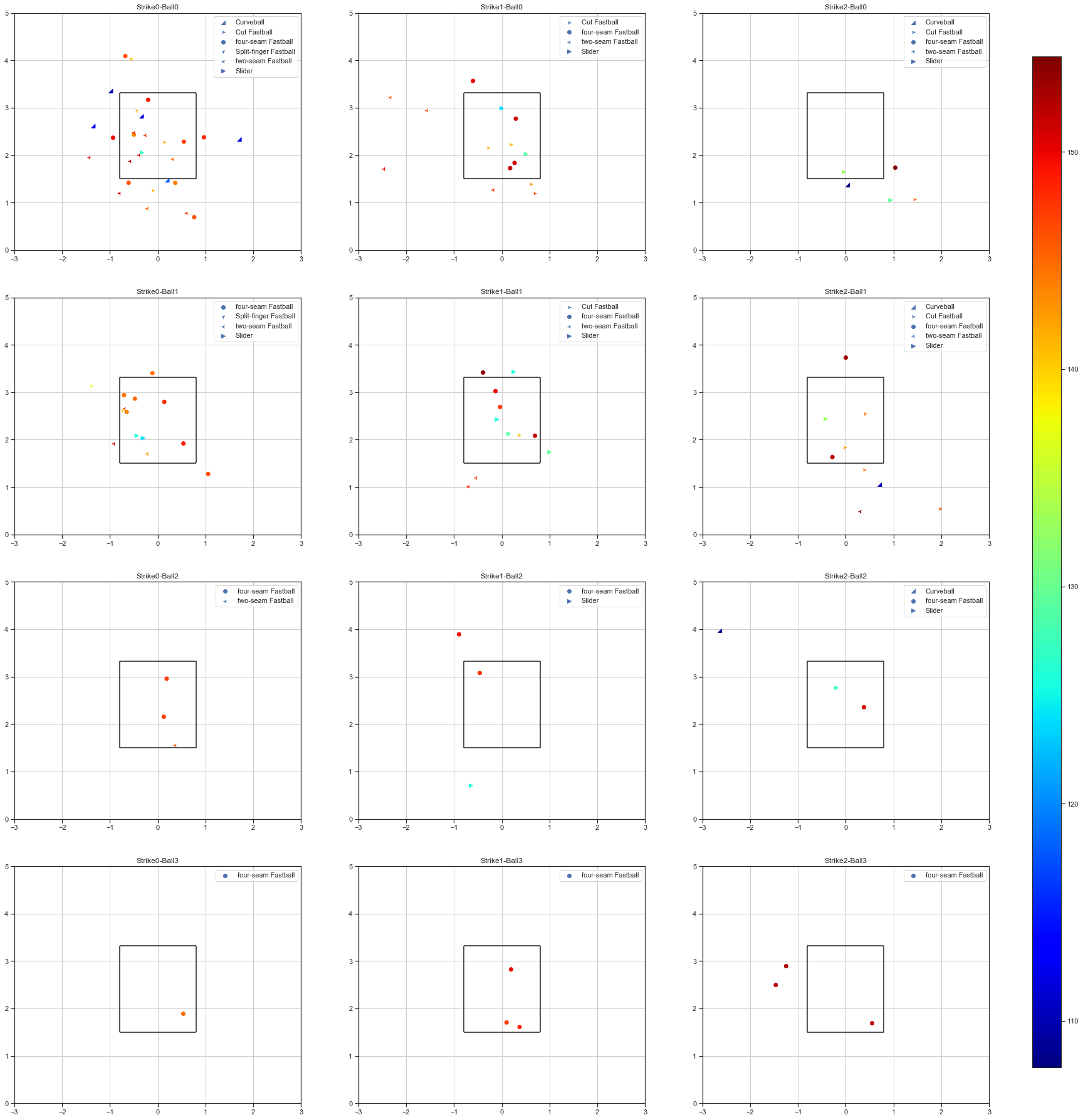

画像を開いて、拡大して見て見ると

カーブは初球に投げる
2-0では右下に投げる
ボールカウントが増えると直球率が高くなる
意外にもカウント2-3では外しに来る
追い込んだとき or　追い込まれた時には配球が右下に集まっている

ように見えますね。

終わりに

弊社ではデータスクレイピングだけでなく、pythonを用いた機械学習やデータビジュアライズなども承っております。
最近流行りのデータサイエンスでソリューションを生み出しましょう。
データコンサルティングのご案内

Pocket

CONTACT

お問い合わせ・ご依頼はこちらから